Fourier series representation for discrete time periodic signals

A discrete time periodic signal \(x[n]\) with fundamental period \(N\), can be decomposed into harmonically related complex exponentials, \(e^{j k \omega_{0} n} ,\) weighted by a set of coefficients, called the spectral coefficients, \({a_k}\), as follows:

\[ x[n] = \sum_{k=<N>}^{} a_{k} e^{j k \omega_{0} n} \quad \text{(Synthesis equation)} \]

where the spectral coefficients are uniquely obtained from

\[ a_{k} = \frac{1}{N} \sum_{n=<N>}^{} x[n] e^{- j k \omega_{0} n}\quad \text{(Analysis equation)} \]

\(<N>\) indicates \(N\) successive integers to cover one full range of fundamental period.

The spectral coefficients, \(a_k\), are periodic with period \(N\), that is, we have \(a_{k}=a_{k+N}, \forall k\in(-\infty,\infty)\).

Let us compute the spectral coefficients of \(x[n]=\sin(0.2 \pi n)\).

This is a periodic signal with period \(N=10\) since \(\omega_0 = 0.2\pi =\frac{2\pi}{N}m\), where \(m, N\) are integers. The smallest value for the fundamental period \(N\) is obtained for \(m=1\), which yields \(N=10\).

It is straightforward to obtain the spectral coefficients of \(x[n]\) by using the Euler’s formula:

\[ x[n] = \sin(0.2 \pi n) = \frac{1}{2j} \left( e^{j 0.2\pi n} - e^{-j 0.2\pi n}\right), \]

which yields \(a_1 = \frac{1}{2j}\) and \(a_{-1} = -\frac{1}{2j}\).

Let us now verify this result using Python in two different ways. First, using the Euler’s formula. It is possible to re-write the function \(x[n]\) in Euler’s form using SymPy’s rewrite function as shown below.

import sympy as sym

n = sym.symbols('n', integer=True)

x = sym.sin(0.2*sym.pi*n)

x.rewrite(sym.exp)  # this line does the trick

\[\displaystyle - \frac{i \left(e^{0.2 i \pi n} - e^{- 0.2 i \pi n}\right)}{2}\]

Next, we will use numpy to directly evaluate the analysis equation:

import numpy as np
N = 10
omega0 = 0.2*np.pi 

x = np.sin(0.2*np.pi*np.array(range(0,N,1))) # the signal 

a = np.zeros(N, dtype=np.complex64)
for k in range(0,N,1): 
    sum = 0
    for n in range(0,N,1): 
        sum += x[n]*np.exp(-1j*k*omega0*n)
    a[k] = np.around(sum, decimals=2)/N
    print("a_{0}={1}".format(k, a[k]))

a_0=0j
a_1=-0.5j
a_2=0j
a_3=0j
a_4=0j
a_5=0j
a_6=0j
a_7=0j
a_8=0j
a_9=0.5j

These values are the same as the ones we obtained above both analytically and using SymPy. The verification is left for the reader as an exercise. (Hint: \(a_k = a_{k+N}\))

Let us apply the numpy method above to another signal: find the spectral coefficients of \(x[n] = 1 + \sin\left(\frac{\pi}{5}n\right) + \cos\left(\frac{2\pi}{5}n + \frac{\pi}{2}\right)\) (Exercise 7.2 in the book). Here is the signal:

N = 10
omega0 = np.pi/5 

ns = np.array(range(0,N,1))
x = 1 + np.sin((np.pi/5)*ns) + np.cos(2*(np.pi/5)*ns + np.pi/2)  # the signal

# plot the signal
from matplotlib import pyplot as plt
plt.stem(ns,x)
plt.xlabel(r'$n$'), plt.ylabel(r'$x[n]$');

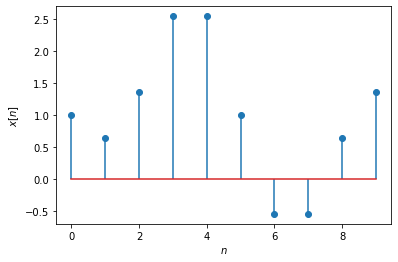
Its spectral coefficients are:

a = np.zeros(N, dtype=np.complex64)
for k in range(0,N,1): 
    sum = 0
    for n in range(0,N,1): 
        sum += x[n]*np.exp(-1j*k*omega0*n)
    a[k] = np.around(sum, decimals=2)/N
    print("a_{0}={1}".format(k, a[k]))

a_0=(1+0j)
a_1=(-0-0.5j)
a_2=0.5j
a_3=(-0+0j)
a_4=(-0+0j)
a_5=(-0+0j)
a_6=-0j
a_7=-0j
a_8=-0.5j
a_9=0.5j